3.1 量子位的概念(Qubits)
量子位定義
量子位(Quantum Bit,簡稱Qubit)與傳統計算中的比特(Bit)有著根本的不同。
傳統比特在任一時刻只能處於兩種明確的狀態之一:0或1。
而量子位則利用量子力學的原理,能夠同時處於0和1的狀態,這種狀態被稱為叠加態。
傳統的位元(Bit)
在傳統的數位計算中,基本的資料單位稱為位元(Bit),它是Binary Digit(二進制數字)的縮寫。
一個位元在任何時刻都只能代表一個狀態:0或1。
這種二進制的表示方式是現代電腦運算的基礎,每個位元的狀態可以透過不同的物理媒介來實現。
在大多數現代電腦中,這些位元是通過晶體管(Transistor)來實現的。
晶體管是一種半導體裝置,能夠進行開關控制,從而控制電流的流動。
在一個簡單的情況下,當晶體管導通(開啟)時,它可以代表位元的「1」狀態;
當晶體管截止(關閉)時,則代表位元的「0」狀態。
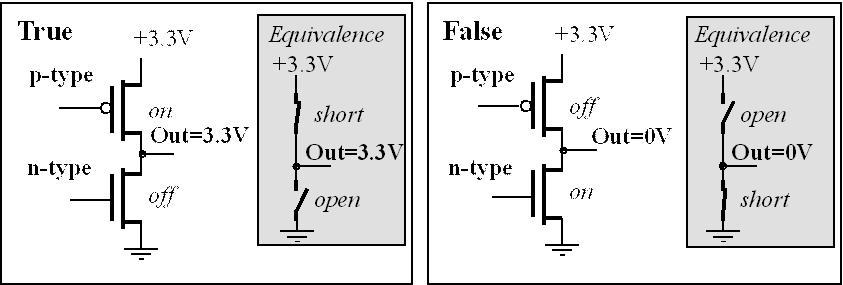
這裡的0與1,是人類給transistor兩種不同狀態加上去的概念,
transistor內部並沒有一個可數的甚麼東西可以讓你去數它有零個還是一個。
0與1是一組抽象的概念,分別用來對應到transistor的關閉與開啟的兩種狀態。
通過成千上萬甚至數十億的晶體管的組合,現代電腦可以進行複雜的計算和資料處理。
舉例來說,如果你把8個transistor放在一起,這就組成了8 bits, 也就是1 byte。
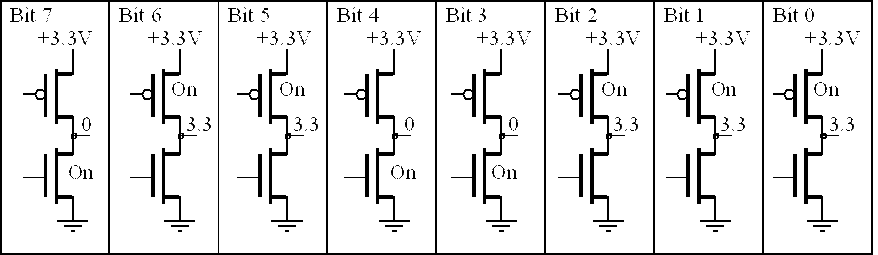
上圖並不代表在你電腦任何地方的每一個bit背後就是只有一個transistor,
隨著位元載體的不同(SRAM, DRAM, ...),1個bit背後可能是更複雜的實作。
這些複雜的實作就讓EE(electrical engineering)的人去煩惱就好了,
對於CS(computer science)的人來說,需要了解的就是資料的最小單位是1 bit,
所�有的運算都是基於bits衍生的。
許多人會說8 bits對應到的是0~255這兩百五十六個數字,這不太正確。
這8個bits,可以用來表示成256種不同的...東西。
更明確的說法是,這8個bits在電腦中的表示可能為00000000、00000001、 ...、11111111,總共256種。
那上圖中的01100111代表甚麼呢?答案是都可以,只要大家同意就好。
當我們想要討論數字的時候,01100111我們大家會把它當成:16進位的0x67、十進位的103。
當我們想要用它表示我們在螢幕上印出來的字母時,01100111會印出英文字母的小寫f。
當我們在討論intel指令集的時候,01100111會被當成一種prefix。
所以說,8 bits的資料可以在每一個應用中表現出256種不同的可能性(00000000、00000001、 ...、11111111),
這每一種可能性所代表的意義,定義於應用的場景中。
量子的位元(Qubit)
量子位元,或稱為�量子比特(Qubit),是量子計算中的基礎資訊單位。
與傳統計算的比特(Bit)只能表示0或1的二元狀態不同,量子位元採用量子力學的原理,能同時處於0和1的狀態,這種現象被稱為量子叠加。
這一特性使得量子位元能在同一時間攜帶比傳統比特更豐富的資訊。
量子位元的特殊性質源自於兩個核心概念:量子叠加(superposition)和量子糾纏(entanglement)。
量子叠加讓量子位元不僅能處於純粹的0或1狀態,還能存在於這兩種狀態的叠加中,彷彿同時存在於兩種狀態,但是如果我們去觀察(measure)那個量子,該量子的狀態就會坍縮(collapse)到0或1之中的一個狀態。
量子糾纏則是一種更為神秘的現象,兩個或多個量子位元可在物理上相距甚遠,卻能瞬間相互影響,一個量子位元的變化能即時影響另一個量子位元。
實現量子位元的方式有多種,如離子陷阱(trapped ions)、超導電路(superconducting circuits)、光子(photons)、自旋電子(spin electron)等。
每種實現方式都有其優勢和局限性,目前還沒有一種技術在所有方面明顯優於其他技術。
隨著量子計算研究的不斷深入,未來可能出現更高效和穩定的量子位元實現方式。
不同Qubit實現裡面的0與1,它們所對應的背後的物理現象是不相同的。
當你想要知道某台量子電腦的0背後是甚麼物理現象,首先你要問這台量子電腦是trapped ions做的還是甚麼的。
舉例來說,如果是trapped ions,0對應的就是離子的一個特定能級。
儘管不同量子電腦的0與1是不同的實作方式,我們在一般的量子計算的討論上,不會特別去區分它們。
圖形表示上我們會常常看到用一顆電子圓球加上一個方向箭頭,用箭頭向上或向下來表示0或1。
這種表示源自於自旋電子(spin electron)技術,會選用這種呈現��方式是因為電子自旋簡單好理解又好畫圖。
疊加態的圖形表示也會有幾種不同的呈現方式,這個之後我們會介紹。下面先給大家看一個簡單的示範:

- 有些時候你會看到箭頭向上表示0,箭頭向下表示1;
有些時候你會看到箭頭向上表示1,箭頭向下表示0。
這看作者的習慣。
- 不是所有的量子系統都是用自旋電子的技術,不要被圖形表達誤導了。
量子態的表示
狄拉克表示法
在量子計算裡面,
0這個狀態我們會用∣0⟩表示,
1這個狀態我們會用∣1⟩表示。
從現在開始會用比較正式的表示。0與1指的是傳統電腦位元的兩個狀態;而∣0⟩與∣1⟩指的就是量子電腦中位元的狀態,我們不會再用0與1來表示量子位元了。
符號∣ψ⟩我們念作ket psi。
∣0⟩我們讀ket zero,∣1⟩我們讀ket one,∣010⟩我們讀ket zero one zero。
∣0⟩與∣1⟩所對應的物理現象,如前面所述,端看該量子電腦的qubit是用哪種技術實作的。不同量子電腦的實作,都會有兩種狀態可以對應到∣0⟩與∣1⟩。
疊加態量子表示法為∣ψ⟩=c0∣0⟩+c1∣1⟩,其中∣c0∣2+∣c1∣2=1,c0∈C,c1∈C。
∣c0∣2是測量後會是∣0⟩的機率,∣c1∣2是測量後會是∣1⟩的機率,於是∣c0∣2+∣c1∣2=1。
有些時候我們也會用矩陣的方式來表示
∣ψ⟩=[c0c1]。
∣⟩這種表示法我們稱呼它為狄拉克表示法,Dirac notation。狄拉克表示法中,量子態用∣⟩表示,
同時我們為這個量子態定義他的共轭转置(conjudgate transpose)為⟨∣。譬如:∣ψ⟩與⟨ψ∣。
用矩陣表示來看的話,∣ψ⟩=[c0c1],
而⟨ψ∣=[c0∗c1∗]=[c0c1]。
一個複數c=a+bi的共轭複數為a−bi,可以用c∗或c表示。
共轭转置我們會用兩個符號∗T來表示,其中∗表示共轭,T表示转置。或者可以用一個dagger符號†表示。
⟨ψ∣=∣ψ⟩∗T=∣ψ⟩†
[c0∗c1∗]=[c0c1]∗T=[c0c1]†
⟨ψ∣ψ⟩的意思是這兩個矩陣的內積(inner product):
⟨ψ∣ψ⟩=[c0∗c1∗]⋅[c0c1]=c0∗c0+c1∗c1=∣c0∣2+∣c1∣2
布洛赫球面表示法(Bloch Sphere Representation)
布洛赫球面表示法是一種用於描述量子位(qubit)態的幾何方式,它是由瑞士物理學家費利克斯·布洛赫(Felix Bloch)提出的。
在這種表示法中,一個量子位的純態可以被映射到一個半徑為1的球面上的點,這個球面就被稱為布洛赫球面(Bloch Sphere)。
布洛赫球面的北極和南極分別代表了量子位的基態∣0⟩和激發態∣1⟩,而球面上的其他點則表示量子位的叠加態(superposition states)。

給定一個∣ψ⟩=c0∣0⟩+c1∣1⟩,其中c0,c1∈C。布洛赫球面要做的事情就是把∣ψ⟩映射到球面上。
映射到球面的表達方式有兩種,
第一種是用角度(θ,ϕ)來表示,
第二種是用座標(x,y,z)表示。
布洛赫球面的主要優勢在於其直觀性,能夠清晰地展示量子位的態叠加和糾纏(entanglement)現象。
例如,當一個量子位處於叠加態時,其代表點會位於布洛赫球面的赤道上,這意味著它既不是完全的∣0⟩態也不是完全的∣1⟩態,而是這兩種態的某種組合。
布洛赫球面的公式推導
前面我們提到,一個量子狀態的表達方式為∣ψ⟩=c0∣0⟩+c1∣1⟩
這裡我們令c0=x0+ix1∈C,c1=x2+ix3∈C
已知∣c0∣2+∣c1∣2=1
∣c0∣=x02+x12
∣c1∣=x22+x32
那我們要怎麼從(x0,x1,x2,x3)找出一個球面的轉換呢?
下面提出兩種方法給您參考。
方法1
c0與c1是複數,可以用複數的極座標方式來表示c0=r0eiϕ0,c1=r1eiϕ1。因為∣c0∣2+∣c1∣2=1
1=∣c0∣2+∣c1∣2=∣r0eiϕ0∣2+∣r1eiϕ1∣2=r02+r12
複習一下高中數學。
eiθ=cos(θ)+isin(θ)
z=a+bi=reiθ=r(cos(θ)+isin(θ))
∣z∣=a2+b2=∣r∣
因為r02+r12=1,我們可以視為r0=cos2θ,r1=sin2θ,並且再定義ϕ=ϕ1−ϕ0,這樣我們就可以重寫∣ψ⟩
∣ψ⟩=c0∣0⟩+c1∣1⟩=r0eiϕ0∣0⟩+r1eiϕ1∣1⟩=cos2θeiϕ0∣0⟩+sin2θeiϕ1∣1⟩=eiϕ0cos2θ∣0⟩+eiϕ1sin2θ∣1⟩=eiϕ0cos2θ∣0⟩+eiϕ0eiϕ1−iϕ0sin2θ∣1⟩=eiϕ0(cos2θ∣0⟩+eiϕ1−iϕ0sin2θ∣1⟩)=eiϕ0(cos2θ∣0⟩+ei(ϕ1−ϕ0)sin2θ∣1⟩)=eiϕ0(cos2θ∣0⟩+eiϕsin2θ∣1⟩)
因為eiϕ0無法測量,所以可以忽略。於是就可以簡化成下面的式子
∣ψ⟩=cos2θ∣0⟩+eiϕsin2θ∣1⟩
在量子力學中,兩個僅相差一個全局相位因子的態向量被認為描述相同的物理狀態。
具體來說,如果有兩個態向量∣ψ⟩和eiϕ∣ψ⟩,
其中eiϕ是一個複數的全局相位因子,這兩個態向量描述的是同一個物理狀態。
那θ與ϕ如何算出來呢?
首先我們看到∣0⟩的係數表示機率:P(∣0⟩)=cos22θ,同時,P(∣0⟩)=∣c0∣2=x02+x12,
得到θ=2∗arccos(x02+x12)。
至於ϕ,前面提到ϕ=ϕ1−ϕ0。ϕ1與ϕ0怎麼來的呢?他們只是c1與c0在複數平面的角度而已,所以tanϕ1=x2x3,tanϕ0=x0x1。
∣ψ⟩=cos2θ∣0⟩+eiϕsin2θ∣1⟩
θ=2∗arccos(x02+x12)
ϕ=ϕ1−ϕ0=arctanx2x3−arctanx0x1
方法2
∣c0∣2+∣c1∣2=(x02+x12)+(x22+x32)=1
這裡我們可以看出來,要表達∣ψ⟩我們會用到四個變數x0,x1,x2,x3,這四個變數滿足下面關係式
(x02+x12)+(x22+x32)=1
四個變數就是一個四維空間,我們無法在紙上畫出四維空間來表達∣ψ⟩,我們最多只能在紙上畫出三維空間。
於是,我們嘗試將四維空間轉換為三維空間
[c0c1]=[x0+ix1x2+ix3]⟼xyz=2(x0x2+x1x3)2(x0x3−x1x2)(x02+x12)−(x22+x32)(3.1-1)
這裡對應出來的∣ψ⟩=(x,y,z)就在我們上面提到的Bloch Sphere,證明如下:
我們驗證看看∣ψ⟩=(x,y,z)是不是一個單位球面(Unit Sphere)
∣∣ψ⟩∣2=x2+y2+z2=[2(x0x2+x1x3)]2+[2(x0x3−x1x2)]2+[(x02+x12)−(x22+x32)]2=4(x02x22+2x0x1x2x3+x12x32)+4(x02x32−2x0x1x2x3+x12x22)+[(x02+x12)2−2(x02+x12)(x22+x32)+(x22+x32)2]=...=(x02+x12+x22+x32)2=12=1
從這個公式推導可以看出,(x,y,z)是一個半徑為1的球面,這就是我們上面說的Bloch Sphere
常見的量子態
首先我們先來看看∣0⟩。
∣0⟩可以表示成(1+0i)∣0⟩+(0+0i)∣1⟩,所以(x0,x1,x2,x3)=(1,0,0,0)。
帶入公式(3.1-1),
xyz=2(x0x2+x1x3)2(x0x3−x1x2)(x02+x12)−(x22+x32)=001
再來我們看看∣1⟩。
∣1⟩可以表示成(0+0i)∣0⟩+(1+0i)∣1⟩,所以(x0,x1,x2,x3)=(0,0,1,0)。
帶入公式(3.1-1),
xyz=2(x0x2+x1x3)2(x0x3−x1x2)(x02+x12)−(x22+x32)=00−1
| quantum state | (x, y, z) | bloch sphere |
|---|
| ∣0⟩ | (0, 0, 1) | 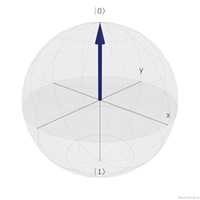 |
| ∣1⟩ | (0, 0, -1) | 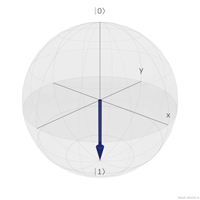 |
接著我們介紹∣+⟩=21(∣0⟩+∣1⟩)與∣−⟩=21(∣0⟩−∣1⟩)。
它們的(x0,x1,x2,x3)=(21,0,±21,0)。
帶入公式(3.1-1),
xyz=2(x0x2+x1x3)2(x0x3−x1x2)(x02+x12)−(x22+x32)=±100
| quantum state | (x, y, z) | bloch sphere |
|---|
| ∣+⟩ | (1, 0, 0) | 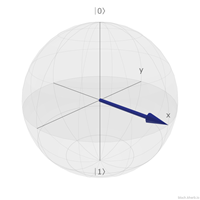 |
| ∣−⟩ | (-1, 0, 0) | 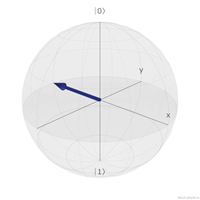 |
最後介紹∣i⟩=21(∣0⟩+i∣1⟩)與∣−i⟩=21(∣0⟩−i∣1⟩)。
它們的(x0,x1,x2,x3)=(21,0,0,±21)。
帶入公式(3.1-1),
xyz=2(x0x2+x1x3)2(x0x3−x1x2)(x02+x12)−(x22+x32)=0±10
| quantum state | (x, y, z) | bloch sphere |
|---|
| ∣i⟩ | (0, 1, 0) | 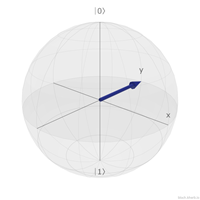 |
| ∣−i⟩ | (0, -1, 0) | 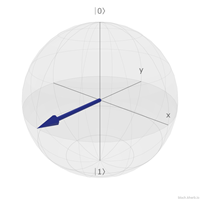 |
x軸上面的是∣+⟩與∣−⟩。
y軸上面的是∣i⟩與∣−i⟩。
z軸上面的是∣0⟩與∣1⟩。
矩陣表示法與bloch sphere並不是一對一的對應關係,畢竟我們是從四度空間(x0,x1,x2,x3)映射到三度空間(x,y,z)。
舉例來說,∣ψ1⟩=∣0⟩,∣ψ2⟩=−∣0⟩,這兩者的差別在於x0等於1或是-1,代入(3.1-1)後,你會發現對應的(x,y,z)都是(0,0,1)。
雖然∣ψ1⟩與∣ψ2⟩的矩陣表示法不一樣,在量子力學中,我們視為一樣的。因為量子態的表達事實上是用Hilbert Space的equivalence class來表示的。
數學上的表示如下
∣ψ1⟩∼∣ψ2⟩⟺∣ψ1⟩=c∣ψ2⟩,c∈CHilbert Space後面會解釋。
從Bloch Sphere逆推回係數x0…x3

給定一個∣ψ⟩,我們知道他的座標(x,y,z),我們要怎麼找回(x0,x1,x2,x3)呢?
從上圖我們可以看到一個任意的∣ψ⟩,它的長度是1,它與z軸的夾角是θ,它在xy平面上的投影長度為sinθ,投影與x軸的夾角是ϕ,
所以我們可以知道
xyz=sinθcosϕsinθsinϕcosθ(3.1-2)
加入公式(3.1-1)我們得到
sinθcosϕsinθsinϕcosθ=2(x0x2+x1x3)2(x0x3−x1x2)(x02+x12)−(x22+x32)
到了這裡,就是解以下的方程式
⎩⎨⎧2(x0x2+x1x3)=sinθcosϕ2(x0x3−x1x2)=sinθsinϕ(x02+x12)−(x22+x32)=cosθ(x02+x12)+(x22+x32)=1
有天分的你,會解出來是
x0x1x2x3=cos(2θ)cos(β)cos(2θ)sin(β)sin(2θ)cos(β+ϕ)sin(2θ)sin(β+ϕ),β∈R(3.1-3)
你可以試著把(3.1-3)代入(3.1-1),你就會得到
sinθcosϕsinθsinϕcosθ,β會被削掉,就是這麼神奇。
裡面會用到三角函數的公式,這裡我推導x給大家看,y與z的推導就不寫了。
x=2(x0x2+x1x3)=2(cos(2θ)cos(β)⋅sin(2θ)cos(β+ϕ)+cos(2θ)sin(β)⋅sin(2θ)sin(β+ϕ))=2cos(2θ)sin(2θ)(cos(β)cos(β+ϕ)+sin(β)sin(β+ϕ))=sin(θ)cos(β+ϕ−β)=sin(θ)cos(ϕ)
sin(x+y)=sinxcosy+sinycosx
cos(x−y)=cosxcosy+sinxsiny
回到最開始∣ψ⟩的矩陣表達式。
∣ψ⟩=[c0c1]=[x0+x1ix2+x3i]=[(cos(2θ)cos(β))+(cos(2θ)isin(β))i(sin(2θ)cos(β+ϕ))+(sin(2θ)sin(β+ϕ))i]=[cos(2θ)(cos(β)+isin(β))sin(2θ)(cos(β+ϕ))+isin(β+ϕ))]=[cos(2θ)eiβsin(2θ)ei(β+ϕ)]=eiβ[cos(2θ)sin(2θ)eiϕ]∼[cos(2θ)sin(2θ)eiϕ]
最後我們得到
∣ψ⟩=cos(2θ)∣0⟩+sin(2θ)eiϕ∣1⟩(3.1-4)
eiθ=cosθ+isinθ
這裡我們總結一下矩陣表達式與Bloch Sphere之間的轉換。
當我們想要從矩陣表達式(x0,x1,x2,x3)轉Bloch Sphere的時候,我們可以用(3.1-1)來得到(x,y,z),同時也可以用(3.1-2)得到θ與ϕ。
當我們想要從Bloch Sphere轉回去的時候,我們可以用(3.1-4)得到矩陣表達式。
測量的影響與態的表示
叠加態
量子叠加原理介紹
叠加態的創建與操控
叠加態在量子計算中的應用
叠加態與概率幅度
糾纏態
量子糾纏的物理基礎
創建和測量糾纏態
糾纏態在量子資訊中的作用
糾纏與非定域性
基態和激發態
基態與激發態的定義
能級躍遷與量子操控
實現基態和激發態的技術
能態在量子計算中的應用









